 While the new Lync Client brings a lot of new functionalities and a complete new look, it isn’t compatible with a OCS 2007 R2 environment. Another downside is that it can’t be installed together with Communicator 2007 on a single machine. When working on both 2007 R2 and Lync 2010 projects, this means the usage of VM’s or uninstall and re-installing a lot, two options which I don’t like personally.
While the new Lync Client brings a lot of new functionalities and a complete new look, it isn’t compatible with a OCS 2007 R2 environment. Another downside is that it can’t be installed together with Communicator 2007 on a single machine. When working on both 2007 R2 and Lync 2010 projects, this means the usage of VM’s or uninstall and re-installing a lot, two options which I don’t like personally.
Out-of-the-box the client will give you an error message when you try to sign in into an OCS 2007 R2 pool, stating that the version is not correct. This tells me there IS some kind of communication, however, it’s being detected and blocked.
After some research I found a way to be able to run the Lync 2010 client on a OCS 2007 R2 environment – simply by bypassing a version check. To bypass this check, you have to create a new registry entry:
Key: HKEY_CURRENT_USER\Software\Policies\Microsoft\Communicator
Name: DisableServerCheck
Type: DWORD
Value: 1 (00000001)
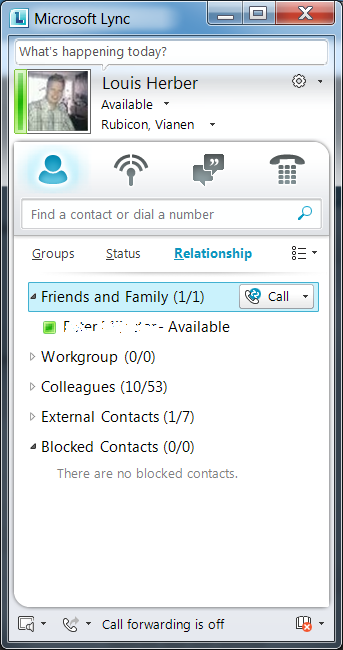
When this entry has been created, the version check will be skipped, and the Lync Client WILL logon to the OCS 2007 R2 environment. Actually, most of the functionalities just work fine! IM, Presence, calling and video work all as espected.
Of course there are some functionalities which don’t work correctly. One of these functionalities is the “Live Meeting” functionality; this is now built-in into the Lync Client, while in the previous version it was a separate client. Installing Lync will uninstall the LiveMeeting plug-ins in outlook as well, disabling you to schedule an old-fashion meeting. But hey, at least now we can connect to both environments with this new client!
!! Please Note!! This is a procedure might work for you, but is not supported in any way by Microsoft. Please don’t use this in your production environment as it *might* lead to data loss or corruption. However I haven’t seen this myself, it is a possibility and in that case you will be on your own …

Works! Thanks a lot. I really missed history feature in OCS 2007
Is not working for me 🙁
Do I need to reboot?
tried this and it’s not working for me too! using win7 64 bit. any other tips?
hello,first of all, thanks for reading my blog. I am using Windows 7 64-bit as well, and this trick is still working. Maybe there is a new version of the client sofware. Can you please mail me with your current version of the Lync 2010 client software and exact error message and/or more information and I’ll try to help you out, and if needed update this article.
the version is 4.07577.0
Hi,
i faced the same issue with Windows7 64-bit but after creating DWORD (32-Bit) value resolved the issue for me. eveything is working normal
AnkurL
Mike,
my version is same as your 4.0.7577.0, creating DWORD (32-bit) resolved the issue. goahead and create 32bit DWORD in windows7 64-bit.
AnkurL
Dear AnkurL,
it indeed needs to be a DWORD (32-bit) value, also on windows 7 64-bit. However I asumed Mike already did that.
64-bit value would be QWORD, by the way.
Then it could be something as a strict client version filtering policy on the server side, I’d already made some suggestions and questions by email to Mike.
Louis Herber
hello! yes, i used DWORD (32-bit value) but it still doesn’t work.
Louis – got your email. might really be some client filtering setup on our servers. too bad =(
I’ve installed the Lync2010 client and all is well, but has anyone else noticed that the address book isn’t working? My client claims that it can’t access the address book because of my browser’s proxy settings (which there aren’t any). Is this common? We’re using Exchange 2010 SP1, OCS 2007 R2, and I’m running Lync2010 client on Win7 32-bit.
doesnt work for me either.
x64 win7 (using VL Lync client, btw).
Dears ,
i hav win 7 64 bit i added the reg key and value 1 like mentioned but doesnt work for me :s any suggestions
also i discoverd something on the OCS FE server the option of Client version filter but i can’t change on it???
please help
Strange that some of you can’t use this “trick”. Please note it is unsupported, but that doesn’t make any difference to my opniion that I find it strange it doesn’t work for you. I use this for quite some time now on several 2007 R2 (and of course Lync) environments with no problems at all.
I don’t think it will be the issue but it could be the Client Version Filtering. When you open the management tool of OCS 2007 R2, right-click your pool. Filtering Tools -> Client Version Filtering, and there you are. Just make sure it’s not enabled, or if you have it enabled for some reason, add an entry for the lync client.
thank you louis for your reply
i cant change ,add or edit in the client version filter it give me the following error
“Unable to save chages to WMI. Exception: (FFFFFFFFF)” and i have all privileges
also in my windows 7 64bit i added the following DisableServerCheck DWARD 32 bit with value data 1 HKEY_CURRENT_USER\Software\Policies\Microsoft\Communicator
do you have any solution for this ??
Regards
ok, interesting… I was able to get the “trick” to work on a cleanly installed Win2k8R2 machine. It does not work from my Win7 x64 machine though… I think the key issue is that the Win7 machine previously had Communicator 2007 R2 installed on it… I fully uninstalled, but I bet it is leaving something in the registry or file system that keeps this simple registry trick/hack from working. BUT I can’t find where… I added the DisableServerCheck key to just about every Communicator related hive I could find, to no avail…
any thoughts?
Well “me”, on the machines which I tested (W7 x64), they had communicator installed at first as well. I am suspecting some update or GPO, as in your case it is obvious it is not the server environment itself.
And haytham, that error message which you get really seems as a rights issue. Do you have the correct privileges in the Active Directory, are you a member of the admin group for OCS, and Domain Administrator just to make sure for any other rights you might be missing. and of course local administrator. You should be able to change the client version filter, seems you are facing some other issue!
I’m sorry I can’t help you further, you’re on your own there as I don’t know anything about your setup, environment or settings. I also can’t think of any thing further what could cause this. But I’d be very interested if you find out what is causing the trouble.
Dear Louis , i solved the problem and it work fine now, what i did is installed the old ocs client, do the registery changes then installed the lync client then it works 🙂
in the beginning i was uninstalling the old client before install the new and was not working i think it need to not unistall the old ocs 2007 client just upgrade it to new ver.
by the way still no work around for the address book sync???
thank you for your nice blog and support
Regards
What haytham mentioned above also worked for me
Running Lync 2010 Client against OCS 2007 R2 as well. Anyone make progress on getting the address book sync? Looks like an LDAP or certificate failure issue? Thoughts?
Pingback: Setup and Install Lync client to communicate to OCS 2007 R2 | Windows Live space
Hey guys
Registry trick works perfectly, but still facing the same problem with address book sync while on OCS 2007 server R2.
‘Cannot synchronize address book information’
your help is much appreciated.
Registry trick works for me. Awsome!
There is no way to ‘fix’ the Address Book download or any other integration issues as using the Lync client with an OCS Front End server is unsupported and was never tested.
By the haytham’s method, It works. Thanks a lot!
Thanks so much!!! Was testing Offfice365 and replaced my OCS client with Lync2010. Then couldn’t connect to OCS to use IM. You are a life saver!!!
did not work with me.
Hi,
With the registry changed, I still have a Lync log-in problem (something like “checking server certificate”). Any idea? Thanks a lot
Sorry, I have not said that I had previously installed OCS 2007 R2 in this Pc, and I could log-in in OCS server. So I understand that certificate was ok, and I have not modify it…
Pingback: Hilfe bei Servern
Try this.. to fix the address sync issue…
http://support.microsoft.com/kb/939530
Pingback: buy office outlook 2010
Thanks, works fine for me. Great tip.
Pingback: Windows Key
1) HKEY_CURRENT_USER\Software\Policies\Microsoft
right click on “Microsoft” and add new “key” name “Communicator”
now you can find Key: HKEY_CURRENT_USER\Software\Policies\Microsoft\Communicator
2) right click on “Communicator” and add new “DWORD” name “DisableServerCheck”
Name: DisableServerCheck
Type: DWORD
Value: 1 (00000001) hex
is er ook een fix voor de lync 2010 versie op de ipad 2?
Mvg, Henk
Thank you very much. This worked. Windows 7 64 bit
Pingback: Nina
The Lync Client cannot conect to MS-Exchange to get more contacts. The error tells nothing.
Anybody has idea?
Regards
Worked for me !! Thank you.. !!
Thanks for this informative article.
There’s a requirement from the client where they want to give a feel of lync client to the higher management so that they convince for the approval for this project of upgrade. Now, lately what’s been decided is upgrade the schema and install one lync server and for that I am supposed to present an Impact analysis which should capture every issue which might occur in future on OCS R2 server as well as to OCS R2 communicator users.
I was thinking to suggest this registry tweak, instead of schema upgrade but I wanted to be sure whether IM and Live Meetings which heavily used in my organization will work perfectly fine with no address book sync issue. Just for the information we are talking about 30K users.
Please suggest, it would be of great help.
Thanks,
Pravin Sangwan
Make sure you are under POLICIES key. On my case there wasn’t a communicator key there and after creating it and adding the dword value it worked perfect. Thank you very much for this..
HKEY_CURRENT_USER\Software\POLICIES\Microsoft\Communicator
Name: DisableServerCheck
Type: DWORD (32 bits)
Value: 1 (00000001)
It’s tricky or just an eye catching thing but at first i did the change on the non-policies key under software.
Is there a solution for the IPad Lync client app to work with the OCS 2007 server?
Hey
I have installed the lync 2010 client on my ipad and my organization runs on OCS 2007 R2 is there any tweaking available on the ipad so that i can access the ocs 2007 environment using lync 2010 client?
Thanks in advance
Pingback: custom access database design
@Henk, @Avi, @Rocky : Lync 2010 Mobile Client uses a totally different mechanism to contact the Lync environment from the OCS 2007 R2 architecture. Even more, a Lync Server environment needs additional installation bits and DNS/Certs/Reverse proxy changes to get the Mobile Client to work. So while we can “trick” the Lync Windows client, we cannot “trick” the Lync Mobile Client.
@ Pravin : I wouldn’t recommend of taking this approach in your production environment. I would rather deploy a Lync pilot pool in co existence with your OCS environment, as per Microsoft best practices. This might take you more time and actions as you mentioned, but it is the only way to show all functionalities in a correct way.
This “trick” where my post is about is only intended for to get a quick view on the look-and-feel of the Lync 2010 client, without having to upgrade your server environment; however some things will not work, or will even break. For instance, IM is working but Live Meetings aren’t. Please also note that this is a non support situation, *if* it would break your OCS database you would be on your own to fix it…
I am facing issues getting back to OCS after installing Lync.
Steps I followed:
1. Installed Lync. It automatically uninstalled OCS
2. Updated the registry to avoid this Lync login issue. After this registry update, Lync worked perfectly.
3. Unistalled Lync
4. Installed Communicator 2007.
5. Tried to login and it’s crashing. Repro on XP as well as Win7. Typical Win7 message – (communicator 2007 has stopped working)
Anyone seen this issue?
Pingback: Using Lync 2010 client in Office Communications Server 2007 R2 environment | John Bontjer
Hi,
I have installed LYNC 2010 client and added registry entry ( as we are running OCS 2007 R2 Pool). Communicator is working fine and my conversations also saving in Outlook ( 2010). However Live Meeting add-on changed to ‘Live Meeting service’ and asking to configure URL. Is there anyway to configure live meeting and working?
Thanks
Venkat
Pingback: Fix OCS 2007 R2 Integration with Outlook 2013 Preview « adamprescott.net
For Lync2013
https://gist.github.com/tormodfj/4117321
Just a note: I’ve found that regardless of registry key, there is capacity to limit to specific versions of Lync. So for example when trying to connect with Lync 4.0.7577.0 I got the error message despite the key being read (confirmed with ProcessMonitor). Running windows update added a security fix to Lync, bringing it to 4.0.7577.4409. The update was sufficient to allow connection.
Pingback: winter springs Florida gym workouts
Just wish to say your article is as amazing. The
clearness to your publish is simply spectacular and that i can think you are knowledgeable on this subject.
Well with your permission let me to take hold of your RSS
feed to stay updated with drawing close post. Thanks a million and please carry on the rewarding work.
Hello?
This is workin, but only administrator user. how to work in local user?
In local user this register way in another location and local user have not edit register permissions.
How to decide this problem? The have all user default register?
Help me!